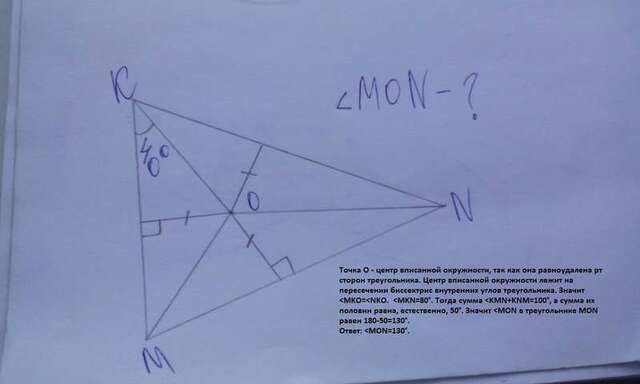
1)4. Точка О - центр вписанной окружности, так как она равноудалена рт
сторон треугольника. Центр вписанной окружности лежит на пересечении
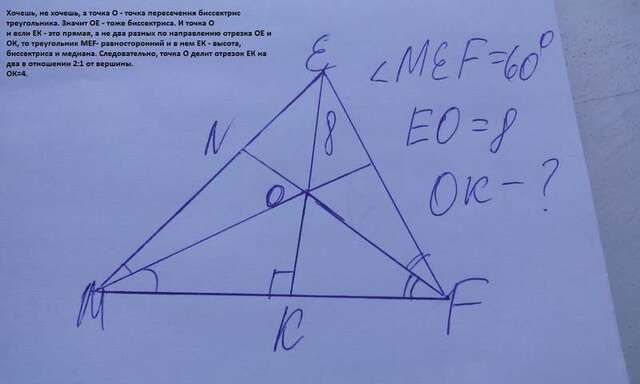
биссектрис внутренних углов треугольника. Значит Ответ: 2) Точка О - точка пересечения биссектрис треугольника. Значит ОЕ - тоже
биссектриса. И точка О
и если ЕК - это прямая, а не два разных по направлению отрезка ОЕ и ОК,
то треугольник MEF- равносторонний и в нем ЕК - высота, биссектриса и
медиана. Следовательно, точка О делит отрезок ЕК на два в отношении 2:1
от вершины.
ОК=4.
ОТВЕТ: ОК=4.
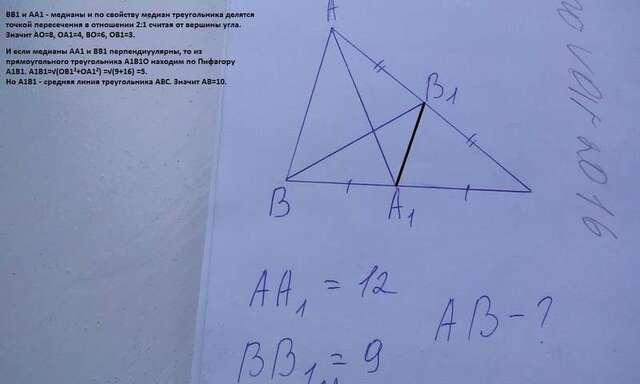
3. АА1 и ВВ1 медианы и по свойству медиан треугольника делятся в точке пересечения на отрезки в отношении 2:1, считая от вершины.
Значит АО=8, ОА1=4, ВО=6, ОВ1=3.
И
если медианы АА1 и ВВ1 перпендикулярны(что совершенно не понятно по рисунку, но должно быть - иначе решения нет), то из прямоугольного
треугольника А1В1О по Пифагору найдем А1В1=√(ОВ1²+ОА1²)=√(9+16)=5.
АА1 - средняя линия треугольника АВС, значит АВ=А1В1*2=10.
ОТВЕТ: АВ=10.
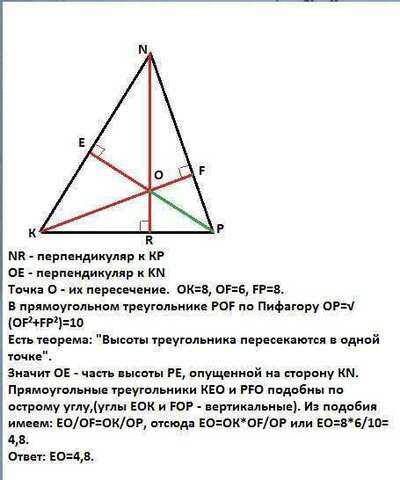
4) Дано: KF -перпендикуляр к NP
NR - перпендикуляр к КР
ОЕ - перпендикуляр к KN
Точка О - их пересечение. ОК=8, ОF=6, FP=8.
В прямоугольном треугольнике РОF по Пифагору ОР=√(OF²+FP²)=10
Есть теорема: "Высоты треугольника пересекаются в одной точке".
Значит ОЕ - часть высоты РЕ, опущенной на сторону КN.
Прямоугольные треугольники КЕО и РFO подобны по острому углу,(углы ЕОК и
FOP - вертикальные). Из подобия имеем: ЕО/OF=ОК/ОP, отсюда ЕО=ОК*ОF/ОP
или ЕО=8*6/10=4,8.
Ответ: ЕО=4,8.