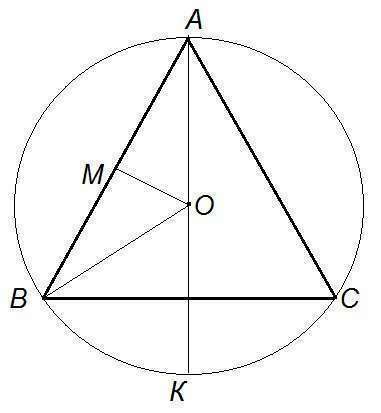
Смотрите рисунок. Нахождение стороны квадрата сводится к нахождению диаметра окружности. О-центр окружности. АК её диаметр. ОМ - перпендикуляр на АВ. АО и ВО - радиусы окружности. Значит ΔВАО - равнобедренный. В таком треугольнике перпендикуляр, опушенный из угла при равных сторонах является, так же и медианой. Значит ВМ = АМ = АВ/2 = 12√3+2 = 6√3 см. <ОАМ = 30 градусов. Значит МО = АО/2. Примем АО= R. Следовательно МО = R/2. Gо теореме Пифагора имеем АМ²+ОМ² = АО². Или (6√3)² +(R/2)² = R². Или 36*3 + R²/4 = R². Приведя к общему знаменателю имеем. 36*12 = 3R². Или 12*12=R². Отсюда R = 12 см.<br> Сторона квадрата, описанного вокруг этой окружности, равна её диаметру = 2R = 2*12 = 24 см.