Помогите, пожалуйста Исследуйте функцию у= 1/|x| План: 1. Область определения, область...

25 просмотров

Помогите, пожалуйста
Исследуйте функцию у= 1/|x|
План:
1. Область определения, область значений
2.Четность(нечетность), периодичность
3.Нули функции
4.Промежутки знакопостоянства
5.Промежутки возрастания, убывания
6.Наибольшее и наименьшее значение

Алгебра Nikamart3494_zn (81 баллов) 03 Апр, 18 | 25 просмотров

Дан 1 ответ

Правильный ответ

$y= \frac{1}{|x|}$

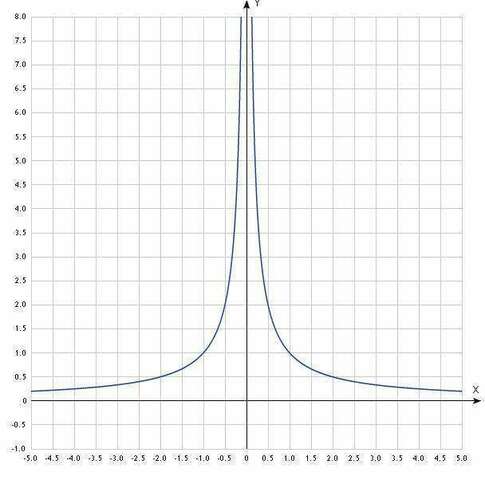
1) ООФ: D(x)=(-бесконечность; 0)U(0; +бесконечность)
ОЗ: E(y)=(0; +бесконечность)
2) $y(-x)= \frac{1}{|-x|}=\frac{1}{|x|}=y(x)$ - функция четная.
Не периодическая
3) Нулей нет, т.к. график не пересекает ось абсцисс (Ох)
4) На всей числовой оси функция принимает положительные значения.
5) При х∈(-бесконечность; 0) - функция возрастает,
при х∈(0; +бесконечность) - функция убывает.
6) Нет, т.к. функция неограничена.

kalbim_zn (63.2k баллов) 03 Апр, 18