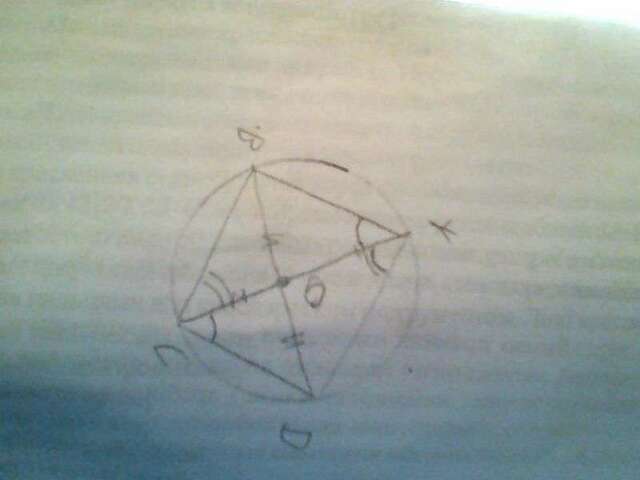
Буду доказывать через треугольники и правило секущей.
если диагонали АС и BD являються диаметрами. следовательно АО ВО ОС ОD есть радиусы. следовательно АО=ВО=ОD=OC.
рассмотрим теругольники AOB BOC COD и AOD:
они есть равноберденные( АО=ВО=ОD=OC как радиусы) следовательно
теругольники AOB BOC COD и AOD равны между собой и равнобедренны.
расмотрим теперь треугольники AOB и COD угл OAB и OCD равны( так как рывны и сами треугольники. по правилам секущей , проходящей через 2 прямые , прямые AB и CD паралельны. ч и требовалось доказать.