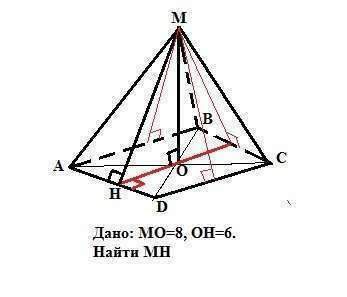
Точка М равноудалена от сторон ромба (основания пирамиды АВСDM), значит вершина М этой пирамиды проецируется в центр основания.
Центр основания (ромба) делит высоту ромба пополам.
Тогда в прямоугольном треугольнике МOH искомое расстояние МН найдем по Пифагору: МН=√(МО²+ОН²), где МО - расстояние от точки М до плоскости ромба, а ОН - половина высоты ромба.
Тогда МН=√(8²+6²)=10.
Ответ: искомое расстояние равно 10.