Длина диагонали основания прямоугольного параллепипеда равна 10 см , его длина 8 см , а...

Question

Длина диагонали основания прямоугольного параллепипеда равна 10 см , его длина 8 см , а угол между диагональю куба и плоскостью основания равна 45 градусов . Определите обьём прямоугольного параллепипеда.

Comments

Пока нет ответов, Вы можете дать более точно условие. Так, как оно дано в учебнике ( или другом источнике)

---

Это всё что есть

---

Если "его длина 8 см" при диагонали 10 - это точно не куб. Скорее всего основание - прямоугольник с диагональю 10 и стороной 8. Тогда ширина основания=6, высота=диагонали основания=10. Проверьте все же условие. Должно быть "угол между диагональю параллелепипеда и плоскостью основания

---

Очень может быть.

---

Если перед решением указать, что в условии явно ошибка и повторить чуть измененное условие ( вместо куб- параллелепипед), т.к. и дальше требуется определить объем параллелепипеда, думаю, можно.

Answer 1

 В формулировке задания допущена ошибка и решение добавлено к задаче с такой (измененной) формулировкой: "Длина диагонали основания прямоугольного параллелепипеда равна 10 см , его длина 8 см , а угол между диагональю параллелепипеда и плоскостью основания равен 45 градусов. Определите объем прямоугольного параллелепипеда."
 Решение:
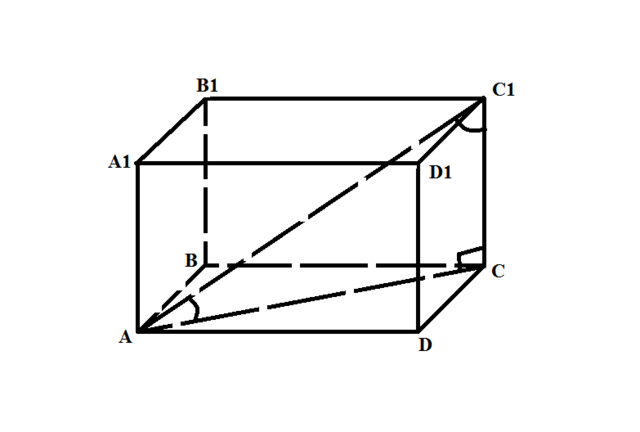
Рассмотрим треугольник AC₁C (см. приложение): угол С₁СА - прямой, а угол С₁АС = 45° по условию. Значит, угол AC₁C = 45° и АС = СС₁ = 10 см.
Рассмотрим треугольник ACD: угол ADC - прямой, АС =10 см, а АD = 8 см, значит, СD =  см.
Объем параллелепипеда равен произведению трех его измерений (AD, DC, CC₁): 8*6*10 = 480 см³.
Ответ: 480 см³

---