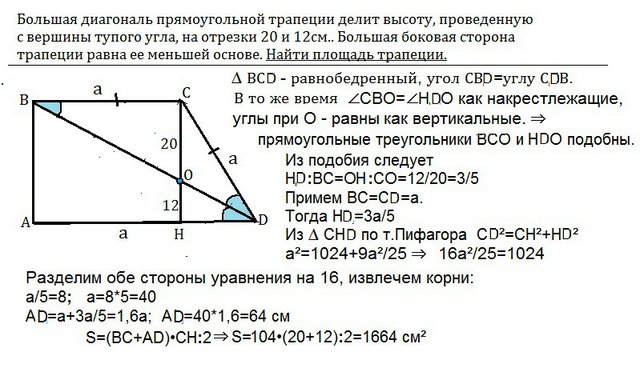
Пусть данная трапеция – АВСD.
СН - высота. Диагональ ВD пересекает СН в точке О, СО=20 см, ОН=12 см.
ВС=СD.
∆ ВСD - равнобедренный, ⇒ угол СВD=углу СDВ.
В то же время ∠СВО=∠НDО как накрестлежащие при пересечении параллельных прямых секущей, углы при О - равны как вертикальные. ⇒ прямоугольные треугольники ВСО и НDО подобны. .
Из подобия следует
HD:ВС=ОH:СО=12/20=3/5
Примем ВС=СD=а.
Тогда НD=3а/5
Из ∆ СНD по т.Пифагора
СD²=СН²+НD²
а²=1024+9а²/25
16а²/25=1024
Разделим обе стороны уравнения на 16, извлечем корни:
а/5=8
а=40 см
АD=а+3а/5=1,6а
АD=40*1,6=64 см
S=(BC+AD)•CH:2=104•(20+12):2=1664 см²