Во-первых, найдем границы площади, то есть точки, в которых график пересекает ось абсцисс.
-x^3 + ax^2 = 0
x^2*(-x + a) = 0
x1 = x2 = 0, x3 = a
Значит, в точке 0 у нас экстремум, а в точке а - пересечение.
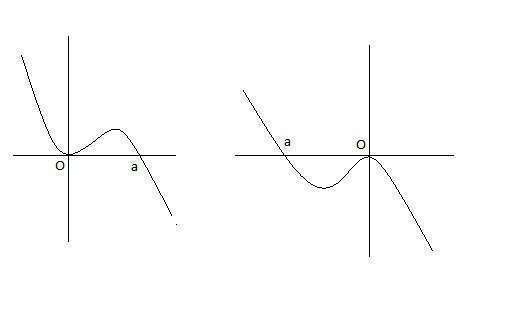
График может иметь один из двух видов, показанных на рисунке, в зависимости от знака числа а.
В обоих случаях площадь - это интеграл.
1) a > 0
S = Int(0, a) (-x^3 + ax^2) dx = (-x^4/4 + ax^3/3) | (0, a) =
= -a^4/4 + a*a^3/3 + 0 - 0 = a^4*(-1/4 + 1/3) = a^4/12 = 4/3
a^4 = 12*4/3 = 16
a = 2
2) a < 0
Здесь область находится под осью Ох, поэтому интеграл получится отрицательным. Но площадь положительна, поэтому берем модуль.
S = Int(a, 0) (-x^3 + ax^2) dx = |(-x^4/4 + ax^3/3)| | (a, 0) =
= |-0 + 0 + a^4/4 - a*a^3/3| = |a^4*(1/4 - 1/3)| = |a^4/12| = 4/3
a^4 = 16
a = -2