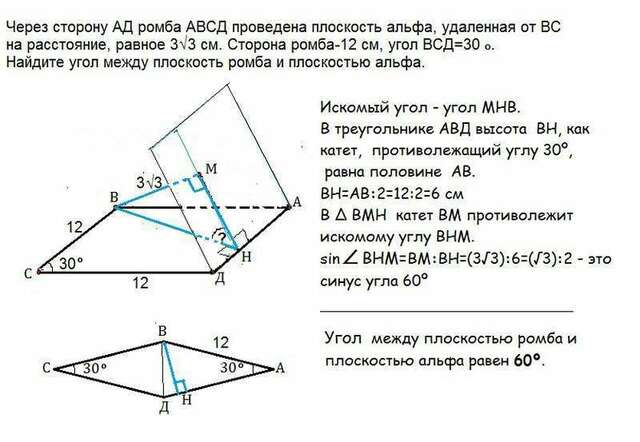
Через сторону АД ромба АВСД проведена плоскость альфа, удаленная от ВС на расстояние, равное 3√ 3 см. Сторона ромба-12 см, угол ВСД=30º. Найдите угол между плоскость ромба и плоскостью альфа
ВС ║АД, ⇒ ВС║α
АД ∈ плоскости α, и расстояние от ВС до плоскости равно длине отрезка их общего перпендикуляра (свойство).
Угол между плоскость ромба и плоскостью α -двугранный угол, и его величина определяется градусной мерой линейного угла.
В данном случае это величина угла, который получится, если из точки Н к АД— линии пересечения плоскости ромба и плоскости альфа, —провести перпендикуляры в обеих плоскостях.
Пусть Н - основание высоты ромба, проведенной из В к АД, а НМ перпендикуляр к АД в плоскости альфа. (см. рисунок)
Искомый угол - угол МНВ.
В треугольнике АВД высота ВН как катет, противолежащий углу 30º, равна половине гипотенузы АВ.
ВН=АВ:2=12:2=6 см
В ∆ ВМН катет ВМ противолежит искомому углу ВНМ.
sin∠ВНМ=ВМ:ВН=(3√3):6=(√3):2 - это синус угла 60º
Угол между плоскость ромба и плоскостью альфа равен 60º.