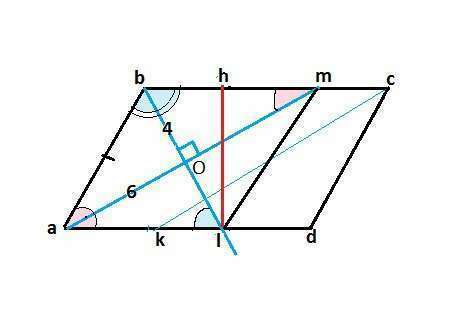
В параллелограмме abcd биссектрисы углов abc и bcd пересекают основание ad в точках l и k соответственно. Известно, что ad=3/2 ab, bl=8, ck=12. Найдите площадь параллелограмма.
--------------
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Следовательно, биссектрисы этих углов пересекутся под углом 90°
В параллелограмме противолежащие углы равны.
∠bad=∠bcd , следовательно, биссектрисы этих углов параллельны и равны. Проведем биссектрису am=ck=12
Биссектрисы bl и am пересекутся в точке О под прямым углом.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник (доказать сумеете).
ab=al
ab=bm
am ⊥ bl ⇒ параллелограмм abmk- ромб.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Так как стороны ромба равны, то
4аb²=bl²+am²
4аb²=8²+12²=64+144=208
ab²=52
ab=2√13 ad=3/2 ab ⇒ ad=(2√13)*3/2=3√13
Площадь ромба равна половине произведения его диагоналей.
S abml=8*12:2=48
Высота параллелограмма abcd является и высотой ромба abml, это отрезок hl, проведенный перпендикулярно стороне ромба.
S abmd=lh*bm
lh=S:bm
lh=48: 2√13=24:√13
Площадь параллелограмма равна произведению высоты и стороны, к которой она проведена.
S abcd=hl*ad
S abcd=(24:√13)*3√13=72 (единиц площади)