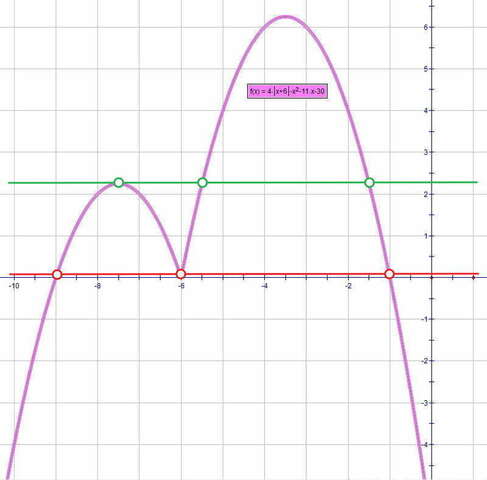
График состоит из двух частей... двух парабол (ветви вниз)))
ключевой точкой является х = -6 ---корень под-модульного выражения...
по определению модуля:
|x+6| = x+6 для x>= -6
|x+6| = -x-6 для x< -6
получим две функции (параболы):
y = -x^2 - 7x - 6 для x>= -6
y = -x^2 - 15x - 54 для x< -6
ровно три общие точки с прямой, параллельной оси ОХ,
получатся в "вершине левой параболы" и в точке х = -6
если х = -6, у = -(-6)^2 - 7*(-6) - 6 = -36+42-6 = 0
y=0 ---это первая прямая, удовлетворяющая условию, ---> m=0
для параболы y = -x^2 - 15x - 54 координаты вершины:
х0 = -b/(2a) = 15/(-2) = -7.5
y0 = -(-7.5)^2 - 15*(-7.5) - 54 = -(225/4)+(225/2)-54 =
= (450-225)/4 - 54 = (225/4) - 54 = (225 - 216)/4 = 9/4 = 2.25 ---> m=2.25