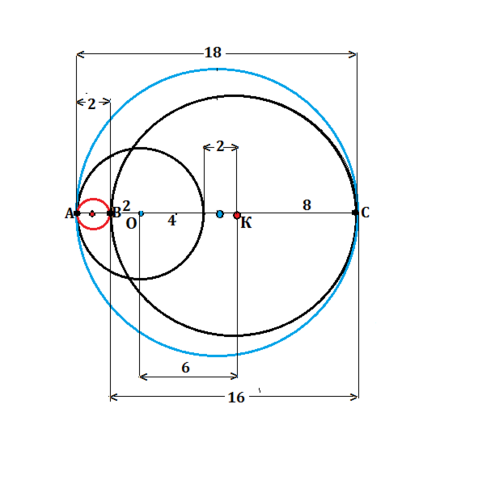
Рисунок здесь - основа решения задачи.
Две первые окружности накладываются друг на друга и пересекаются, поскольку расстояние между их центрами меньше суммы радиусов.
ОК=6
Третья окружность -самая маленькая- расположена между окружностью (К) и окружностью (О), и касается меньшей окружности в точке В и большей- в точке А.
ВК=8, ОК=6, ⇒ОВ=АВ=2
Диаметр АВ самой маленькой окружности равен 2, ее
радиус =1.
Вторая окружность из тех, что касаются одновременно двух первых, "вобрала" в себя три предыдущих и касается окружности с радиусом 4 в точке А, окружности с радиусом 8 в точке С ( с противоположной стороны от К)
Она - самая большая и её диаметр равен АВ+диаметр окружности с радиусом 8, т.е.
АС=2+16=18, и
ее радиус равен 9.