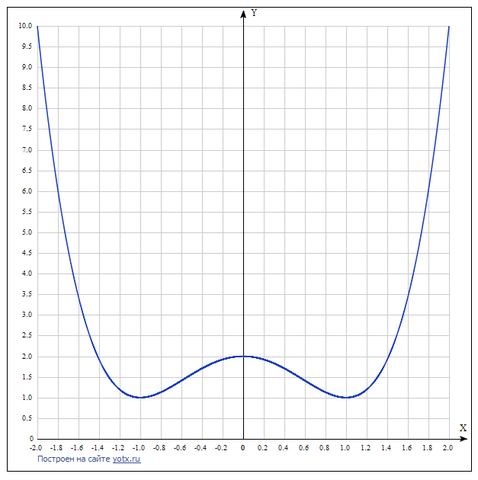
Y=x⁴ -2x²+2
1) Область определения функции:
D(y)=(-∞; +∞)
2) Область значений функции:
Е(у)=(-∞; +∞)
3) Четность или нечетность функции:
у(-х)=(-х)⁴ - 2(-х)²+2=х⁴-2х²+2
Так как у(-х)=у(х), то функция является четной. График функции симметричен относительно оси ОУ.
4) Точки пересечения графика с осями:
ОХ: у=0
х⁴-2х²+2=0
Пусть х²=t
t²-2t+2=0
D=4-8=-4<0<br>График не пересекает ось ОХ.
ОУ: х=0
у=0⁴-2*0²+2=2
5) Промежутки возрастания и убывания функции и точки экстремума:
у' = 4x³ -4x=4x(x²-1)=4x(x-1)(x+1)
4x(x-1)(x+1)=0
x=0 x=1 x=-1
- + - +
-------- -1 --------- 0 ----------- 1 --------------
При х∈(-∞; -1]U[0; 1] функция убывает.
При х∈[-1; 0]U[1; +∞) функция возрастает.
х=-1 - точка минимума.
Уmin=(-1)⁴ - 2(-1)²+2=1-2+2=1
x=0 - точка максимума.
Уmax=0⁴-2*0²+2=2
x=1 - точка минимума.
Уmin=1⁴-2*1²+2=1-2+2=1
6) Точки для построения графика:
х| -2 | -1 | 0 | 1 | 2
y| 10| 1 | 2 | 1 | 10