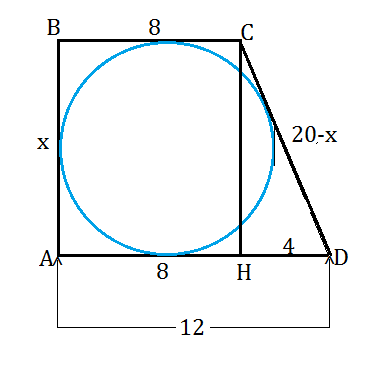Вокруг окружности можно описать четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны.
Трапеция АВСD - четырехугольник. ⇒
АD+BC=AB+CD
АD+BC=20
AB+CD=20
Пусть
АВ=х.
Тогда
CD=20-x⇒
Опустим из С высоту на большее основание и получим треугольник СНD,
в котором
НD=12-8=4
CH=AB=
x
CD=20-x
По т.Пифагора
НD²=CD²=CH²
16=400-40x+x²-x²
40x=384
x=9,6
Высота трапеции равна диаметру вписанной в нее окружности.
D=9,6
r=9,6:2=
4,8