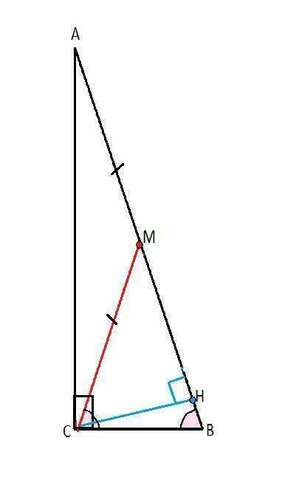
Пусть дан треугольник АВС, где
С=90°, СН - высота, АВ=4 СН по условию.
Проведем медиану СМ.
Медиана прямоугольного треугольника, проведенная из прямого угла, равна половине гипотенузы.
СМ=АВ:2=2 СН
Треугольник СМВ - равнобедренный ( СМ=МВ)
Угол МСВ=угол МВС
В прямоугольном треугольнике МНС катет СН равен половине гипотенузы СМ.
Катет, равный половине гипотенузы, противолежит углу 30° (из теоремы о катете, противолежащем углу 30°)
Сумма углов треугольника равна 180°
Угол МСВ=угол МВС=(180°-угол СМВ):2=(180°-30°):2=75°
Сумма острых углов прямоугольного треугольника равна 90°
Тогда в треугольнике АСВ
угол А=90°-75°=15°