Водный бассейн, ширина которого а=4 м, разделен перегородкой. С одной стороны уровень...

Question

156 просмотров

Водный бассейн, ширина которого а=4 м, разделен перегородкой. С одной стороны уровень воды относительно дна h1 =3 м, с другой - h2 =1 м. Найти силу F, действующую на перегородку.

Напишите пожалуйста с подробным решением, нужно понять как решается. Заранее спасибо!

Физика Texpeady53_zn (15 баллов) 03 Апр, 18 | 156 просмотров

Дан 1 ответ

Правильный ответ

Попытаюсь пояснить.
Cначала уточним условие, я так полагаю, что перегородка установлена параллельно ширине, т.о. нам известна ширина перегородки и она равна,
ширине бассейна a.
Дано:
h1=3м
h2=1м
а = 4м
F=?
Решение
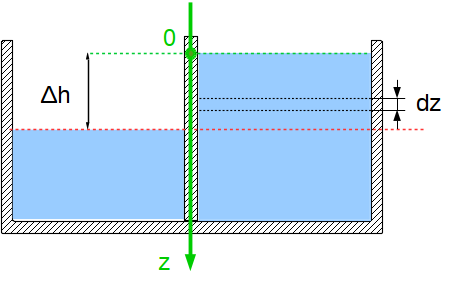
Хорошо чертим рисунок. (см. прилагающийся файл). Тут Δh=(h2-h1). Поясним зачем так. На перегородку действуют силы давления воды слева и справа. Давление воды, расположенной ниже уровня поверхности воды в левой части бассейна компенсируется силой со стороны воды, находящейся на том же уровне в правой части бассейна. (Так несколько сумбурно главное думаю понятно). Нужно найти только силу действующую на перегородку со стороны той части воды справа, уровень которой превышает уровень поверхности воды слева.
Что такое давление, это сила действующая на единичную площадь (обычно 1м^2 ) поверхности. Т. е , зная давление p и площадь поверхности S, можно определить силу F.
$F=p*S$
Но так совсем просто просто будет только тогда, когда давление действующее на поверхность в каждой точке будет одинаковым.
В нашем случае давление будет зависеть от глубины. Поэтому поступим так, как обычно и поступают в подобных случаях.
Для начала зададим систему координат. Ось Z направим вниз, начало координат Z=0 установим в точке на уровне поверхности воды в правой части бассейна.
Выделим "достаточно тонкий" слой толщиной dz, такой что в пределах этого слоя давление можно считать постоянным. С учетом нашей системы координат давление p(z) в таком слое, расположенном на глубине z , будет равно:
$p(z)= \rho gz$ (1)
здесь:
$p(z)$ - давление, зависящее от глубины ()
$\rho$ - плотность воды =1000 кг/м^3
$g$ - ускорение свободного падения ≈9,8 м/с^2
z - высота столба жидкости над уровнем где определяется давление (глубина).(благодаря выбору системы координат, значение координаты совпадает с высотой столба).
"Элементарная" сила dF, действующая на часть перегородки dS со стороны слоя жидкости толщиной dz:
$dF=p(z)dS= \rho* g*z*dS= \rho* g*z*a*dz$ (2)
Тут dS - "элементарная" площадка равная ширине перегородки а, умноженной на толщину слоя dz.
dS=a*dz

Теперь, чтобы найти полную силу действующую на перегородки нужно просуммировать все "элементарные" силы по всем "элементарным" площадкам, что в пределе при $dz \to 0$ дает интеграл
$F= \int\limits^{\Delta h}_0 { \rho *g*a*z} \, dz = \rho *g*a\int\limits^{\Delta h}_0 {z} \, dz = \rho *g*a \frac{(\Delta h)^2}{2}$

$F= \rho *g*a \frac{(\Delta h)^2}{2}$ (3)

ВОТ ОНА! Долгожданная формула определяющая силу. Подставляем в (3) числа.
$F= \rho *g*a \frac{(\Delta h)^2}{2} \approx 1000*9,8*4* \frac{(3-1)^2}{2}=4000*9,8* \frac{4}{2}=$ $=8000*9,8=78400$ Н.

Ответ: суммарная сила F≈78400 Н

Exponena_zn (13.2k баллов) 03 Апр, 18