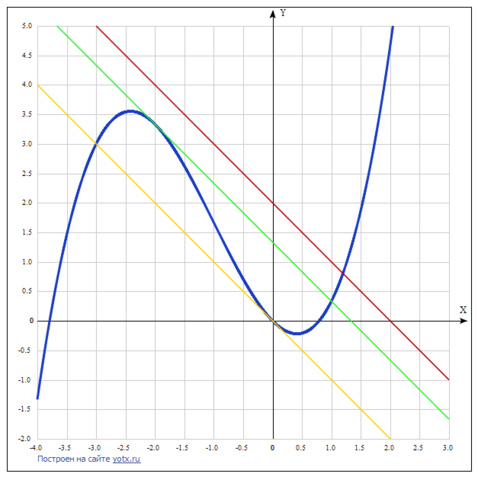
В уравнении касательной вида у = кх + в коэффициент к, показывающий крутизну наклона к оси х, равен производной функции в данной точке.
y' = x² + 2x - 1.
Так как коэффициент к прямой 2 - х, параллельной касательной, равен -1, то, приравняв производную этому значению, определим точку касания:
x² + 2x - 1 = -1
x² + 2x = 0
х(х+2) = 0
Получаем 2 точки:
х₁ = 0
х₂ = -2.
Уравнения касательных находим из равенства координат:
х₁ = 0 у = 0
х₂ = -2 у = (-8/3)+4+2 = 10/3.
Первая касательная проходит через начало координат, поэтому параметр в = 0 и уравнение её у = -х
Для второй касательной определим параметр в:
10/3 = -1*(-2) + в
в =(10/3)-2 = 4/3 и уравнение имеет вид у = -х + (4/3).