Средняя линия треугольника, перпендикулярная высоте, проведенной между данными сторонами, параллельна третьей стороне, к которой высота проведена.
Высота делит данный треугольник на два прямоугольных треугольника, их средние линии – искомые отрезки.
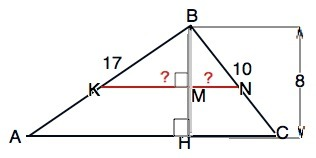
Обозначим треугольник АВС, высоту - ВН.
Из ∆ АВН по т.Пифагора
АН=√(AB²-BH²)=√(17²-8²)=15 см
Из ∆ BCH по т.Пифагора
HC=√(BC²-BH²)=√(10*-8*)=6 см
KM=AH:2=7,5 см
NM=HC:2=3 см
7,5 см и 3 см - отрезки средней линии КN