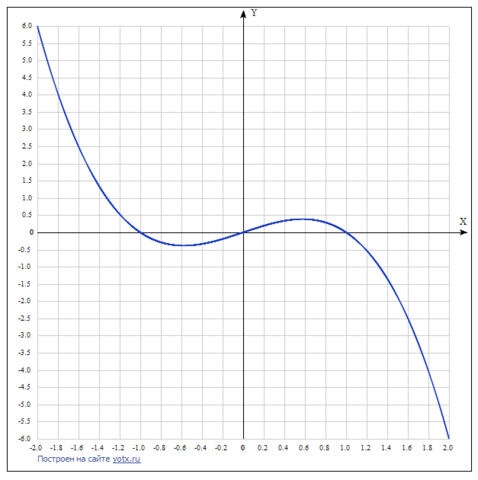
Необходимо найти критические точки с помощью производной, приравняв её 0.
Для того, чтобы найти экстремумы,нужно решить уравнениеd
--(f(x)) = 0
dx (производная равна нулю),и корни этого уравнения будут экстремумами данной функции:d
--(f(x)) =
dx 2
1 - 3*x = 0Решаем это уравнениеКорни этого ур-ния ___
-\/ 3
x1 = -------
3 ___
\/ 3
x2 = -----
3 Зн. экстремумы в точках: ___ ___
-\/ 3 -2*\/ 3
(-------, --------)
3 9 ___ ___
\/ 3 2*\/ 3
(-----, -------)
3 9 Интервалы возрастания и убывания функции:Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:Минимумы функции в точках: ___
-\/ 3
x2 = -------
3 Максимумы функции в точках: ___
\/ 3
x2 = -----
3 Убывает на промежутках[-sqrt(3)/3, sqrt(3)/3]Возрастает на промежутках(-oo, -sqrt(3)/3] U [sqrt(3)/3, oo)
График и более полное исследование функции прилагаются.