У задачи 2 решения.
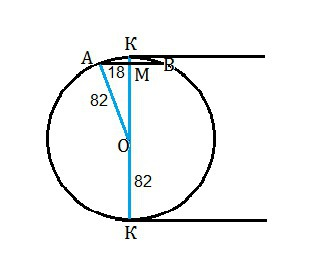
1) Хорда находится между центром окружности и касательной.
Тогда искомое расстояние от хорды до касательной - разность между длиной радиуса, проведенного в точку касания, и расстоянием от центра окружности до хорды.
Пусть К - точка касания, ОК - радиус, проведенный в нее, ОМ - расстояние от центра до хорды ( часть радиуса).
ОМ⊥АВ, т.к. радиус перпендикулярен касательной, а хорда - ей параллельна.
По свойству радиуса, перпендикулярного хорде, он делит ее пополам.
АМ=ВМ=36:2=18.
ОА - радиус. АМ - катет. МО=√(АО²-ОМ²)=80
Отсюда искомое расстояние МК=82-80=2 (ед. длины).
2)
Порядок расположения - хорда, центр, касательная.
Тогда искомое расстояние МК=ОК+ОМ=82+80=162 (ед. длины).