Гипотенуза и катет прямоугольного треугольника соответственно равны 10 см и 6 см. Найти...

Question

Гипотенуза и катет прямоугольного треугольника соответственно равны 10 см и 6 см. Найти наибольшую сторону подобного ему треугольника площадь которого равна 72см²

Answer 1

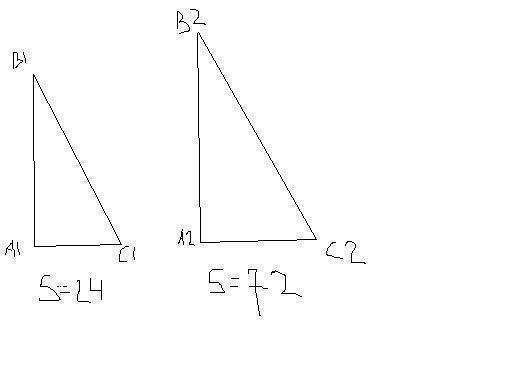
Катет первого прямоугольного треугольника равен Х=√(10²-6²)=8.
Площадь первого треугольника равна половине произведения катетов, т.е
S=1/2*(6*8)=24
Площадь первого треугольника относится к площади подобного как 1:3, т.к
S1/S2=72/24=3.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия, т.е.  катеты относятся:
                      3=(А2В2/А1В1)²        3=(А2В2/6)²     А2В2=6√3  ---катет
                      3= (А2С2/А1С1)²       3=(А2С2/8)²     А2С2=8√3  -----катет
гипотенузы относятся:
                       3=(В2С2/В1С1)²       3=(В2С2/10)²   B2C2=10√3 -------гипотенуза
Проверяем найдём площадь второго треугольника:
S2=1/2*(6√3*8√3)=72
Наибольшая сторона равна 10√3

---

Comments

Хорошее решение! Надоело помогать тем кто не ценит помощь!

---

правда ответ 30 см

---

но всеодно спасибо

---

Почему 30? опять.

---

Надоело свою правоту доказывать! Ответ 10√3 и всё тут.

---

Удалённое решение чушь полная, нет такой теоремы, чтобы стороны подобных треугольников относились как площади 3 к 1.

---

Отношение площадей подобных треугольников равно квадрату коэффициента подобия т.е К^2 а отношение сторон равно коэффициенту подобия K. K=√3 (отношение сторон) а K^2=3 (отношение площадей).

---

Если ваш учитель считает что в ответе 30, то ему на пенсию пора. А уменя 5 лет ФизМата и диплом по Аналитической геометрии на Отлично.

---

То решение не зря удалили а бессмысленно отвечать, чтобы заработать баллы это ФУУУУУУУУУУ