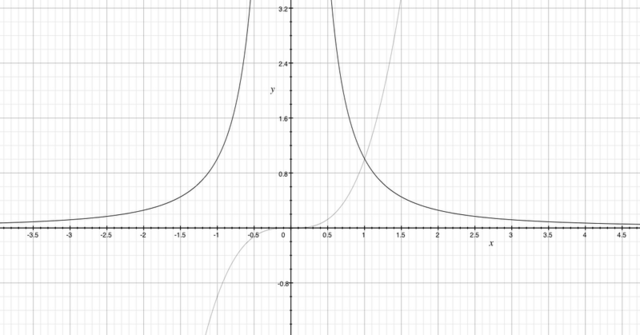
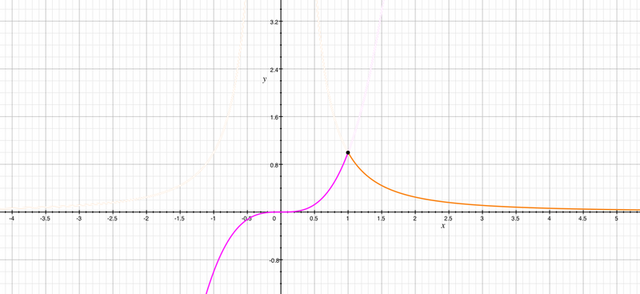
Вот начертил на компьютере оба графика (первое вложение), нужно только x^3 до x=+1 оставить, а 1/(x^2) после x=+1 (смотри второе вложение).
Мы исследуем ("читаем") функцию
1 \end{array}\right." alt="y = \left[ \begin{array}{rl}x^3, & x \leq 1 \\ \frac{1}{x^2}, & x > 1 \end{array}\right." align="absmiddle" class="latex-formula">
Функция монотонно возрастает при x < 1, монотонно убывает при x > 1. При x = 1 имеет особую точку. x = 1 является также точкой максимума функции, при этом y = 1. Пересечения с осью абсцисс — точка x=0,y=0. Пересечения с осью ординат — та же точка x=0,y=0.
