Без взятия производных для определения наибольшего и наименьшего значений функции приходится строить график этой функции.
График функции  можно получить из графика
можно получить из графика  следующим образом:
следующим образом:
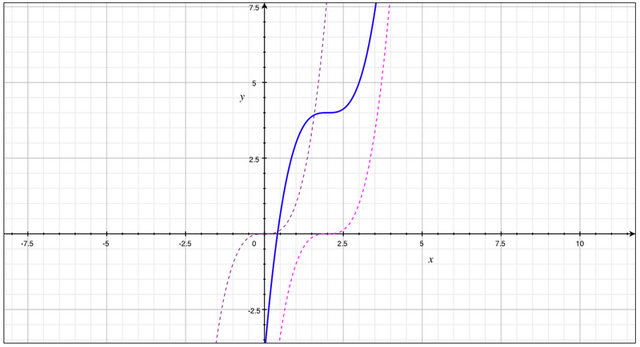
1. График  сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
2. Полученный график y сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
Полученный график функции  показан самым жирным и самым синим на рисунке.
показан самым жирным и самым синим на рисунке.
Из графика видим, что на отрезке ![\left[0;3\right]](https://tex.z-dn.net/?f=%5Cleft%5B0%3B3%5Cright%5D) рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
Итак, ответ.
![min|_{\left[0;3\right]} y(x) = y(0) = \left(0 - 2\right)^3 + 4 = -8 + 4 = -4](https://tex.z-dn.net/?f=min%7C_%7B%5Cleft%5B0%3B3%5Cright%5D%7D+y%28x%29+%3D+y%280%29+%3D+%5Cleft%280+-+2%5Cright%29%5E3+%2B+4+%3D+-8+%2B+4+%3D+-4)
![max|_{\left[0;3\right]} y(x) = y(3) = \left(3 - 2\right)^3 + 4 = 1 + 4 = 5](https://tex.z-dn.net/?f=max%7C_%7B%5Cleft%5B0%3B3%5Cright%5D%7D+y%28x%29+%3D+y%283%29+%3D+%5Cleft%283+-+2%5Cright%29%5E3+%2B+4+%3D+1+%2B+4+%3D+5)