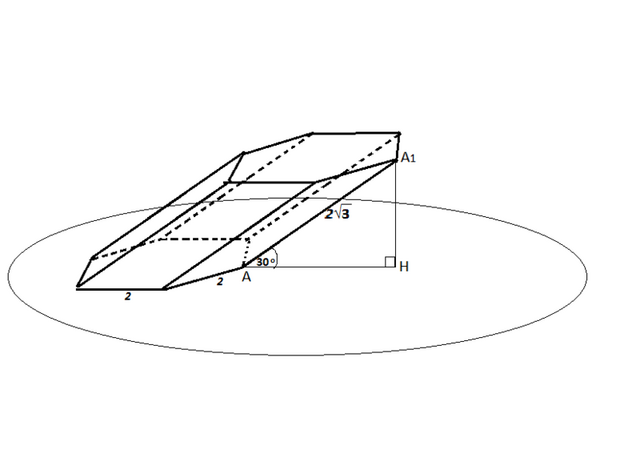
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2√3
и наклонены к плоскости основания под углом 30º.
Объем призмы находят произведением площади её основания на высоту. Основание данной призмы - правильный шестиугольник, который состоит из 6 правильных треугольников со стороной, равной 2.
Площадь правильного треугольника
S=(а²√3):4
S=4√3):4=√3 (ед.площади)
Площадь основания равна в 6 раз больше:
S (o)=6*√3 (ед.площади)
Чтобы найти высоту призмы, опустим из вершины А₁ верхнего основания перпендикуляр А1Н на плоскость, содержащую нижнее основание, и соединим Н с вершиной А нижнего основания.
Треугольник АНА₁ - прямоугольный.
Так как угол НАА₁
=30º, то А₁Н=АА1:2=√3
V призмы=S*H=6*√3*√3=18 (ед. объема)