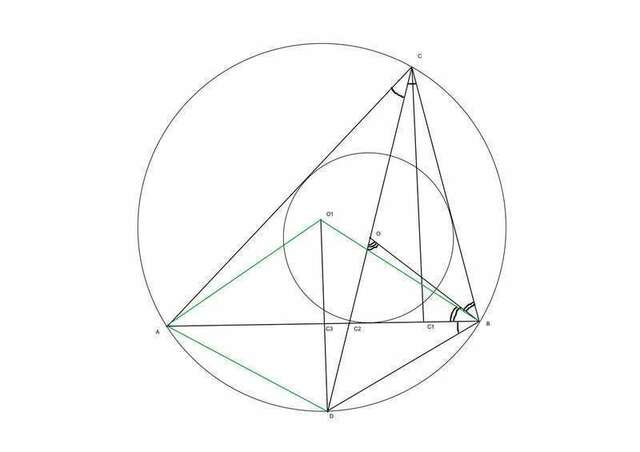
Поскольку все равно, какой буквой в 2) обозначена вершина, из которой выходит биссектриса, я все сведу на чертеж к 1). Конечно, если доказано, что OD = DB = DA для биссектрисы CD, то это будет верно и для двух других биссектрис (со "своими" точками, разумеется).
1) Дуги DB и DA равны, поскольку СВ - биссектриса. => равны центральные углы AO1D и AO1D. => O1D биссектриса в равнобедренном треугольнике, то есть она перпендикулярна основанию AB и делит его пополам. Ну это равносильно тому, что она проходит через середину AB - точку C3, и параллельна высоте CC1.
2) Точка O - точка пересечения биссектрис CO и BO треугольника ABC.
∠DOB = ∠OBC + ∠OCB; как внешний угол треугольника OBC;
∠OBD = ∠OBA + ∠DBA = ∠OBC + ∠ACD = ∠OBC + ∠OCB = ∠DOB;
=> треугольник ODB равнобедренный, OD = DB;
само собой, DB = DA, потому что равны дуги, стягиваемые этими хордами.
все доказано.
это же справедливо для любой из трех биссектрис - AO, будучи продолжена до пересечения с описанной окружностью, даст точку D1, и точно также доказывается D1O = D1C = D1B ...