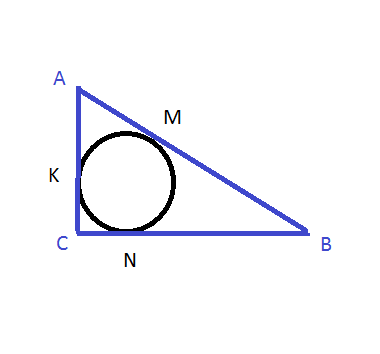
См . рисунок в приложении
Пусть ВМ=10х, АМ= 3х.
По свойству касательной к окружности, проведенной из одной точки,
АМ=АК=3х
ВМ=ВN=10x
АС=АК+КС=3х+4
ВС=ВN+NC=10x+4
АВ=103х=13х
По теореме Пифагора
АВ²=АС²+ВС²
(13х)²=(3х+4)²+(10х+4)²
169х²=9х²+24х+100х²+80х+16
15х²-26х-8=0
D=(-26)²-4·15·(-8)=676+480=1156=34²
x₁=(26+34)/30=2 x₂<0 и не удовлетворяет условию задачи<br>
АС=3х+4=3·2+4=10
ВС=10x+4=10·2+4=24
АВ=13х=13·2=16
Ответ. 10 см, 24 см, 26 см