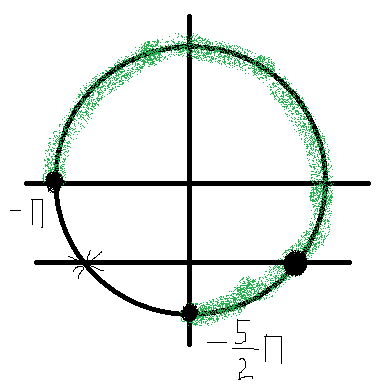Cos²x-sin²x+5√3sinx+8=0
1-sin²x-sin²x+5√3sinx+8=0
-2sin²x+5√3sinx+9=0
sinx=t
-2t²+5√3t+9=0
D=75-4*(-2)*9=147
t1=(-5√3+7√3)/(-4)=-√3/2, t2=(-5√3-7√3)/(-4)=3√3
sinx=-√3/2
х=(-1)^n * (-π/6) + πn, n∈Z
ИЛИ
sinx=3√3
решений нет, т. к. 3√3>1
отбираем на единичной окружности
смотрите прикрепленное изображение
-2П-П/3=-7/3П