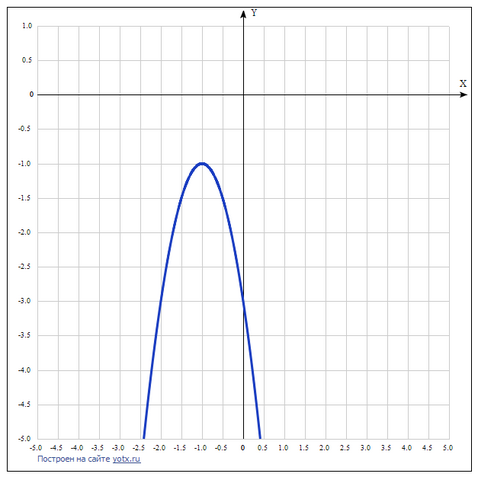
График функции y= -2x² - 4x + m это парабола ветвями вниз (коэффициент при x² отрицателен).
Граничное значение квадратичной функции в виде у = ах² + вх + с, при котором вершина параболы находится на оси Х, равно 0, дискриминант Д при этом равен 0.
Координата вершины параболы Уо = -Д / 4а.
В данной задаче дискриминант Д = в² - 4аm. Отсюда при Д = 0: m = в² / 4а = (-4)² / 4*(-2) = 16 / -8 = -2.
Чтобы график функции y= -2x² - 4x + m НЕ ИМЕЕЛ общих точек с осью абсцисс, вершина параболы должна располагаться ниже оси Х.
При этом коэффициент m - это координата точки пересечения графика оси У при Х = 0.
Поэтому значение m должно быть меньше -2.
Ответ: m < -2.