В двухэлектродной лампе с плоскими электродами напряжение составляет 22 кВ. Электроны...

Question

Дан 1 ответ

Правильный ответ

Попробуем изложить, как мне это видится.
Сила тока равна заряду, протекающему через поперечное сечение проводника в единицу времени.
$I= \frac{\Delta q}{\Delta t}$ (1)
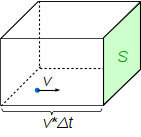
Заряд, протекающий через площадку площадью S за малый временной интерва Δt равен:
$\Delta q=N \cdot e=n \cdot v \cdot \Delta t \cdot S \cdot e$ (2)
N - Количество электронов попадающих в объем V=v*Δt*S
n - концентрация электронов
e - заряд электрона $1,6*10^{-19}$ Кл.
v - Скорость электрона при подлете к пластине (Δt достаточно мал, чтобы считать скорость в течении этого интервала постоянной).
Из (1) и (2) следует, что:
$I= \frac{\Delta q}{\Delta t} =v\cdot S\cdot n\cdot e$ (3)
Замечательно, но концентрация n и площадь S нам неизвестны.
Что можно извлечь из силы. Сила равна (2й закон Ньютона):
$F= \frac{\Delta P}{\Delta t}$ (4) изменению импульса за за время Δt. (Вообще-то производной импульса по времени ).
Вот дальше я вижу некоторый произвол в определении изменении изменения импульса. Если считать, что электрон при прилете весь импульс отдает электроду, то ΔP=mv. Скорость v равна
$v= \sqrt{ \frac{2eU}{m} }$ (5)

$m=9,11 \cdot 10^{-31}$ кг. масса электрона.

Суммарный импульс передаваемый всеми электронами, прилетающими из объема V:
$\Delta P=N \cdot mv=v\Delta t \cdot S\cdot n \cdot mv$
Соответственно сила F:
$F= \frac{\Delta P}{\Delta t}=\frac{v\Delta t \cdot S \cdot n \cdot mv}{\Delta t}=mv^2Sn$ (6)
Вот. Теперь из (6) можно выразить концентрацию n через силу F.
$n= \frac{F}{mv^2S}$ (7)
Теперь, если (7) подставить в (3) получим:
$I =\frac{vSeF}{mv^2S}= \frac{eF}{mv}$ (8)
Скорость из (5) подставляем в (8).
$I =\frac{eF}{m \sqrt{ \frac{2eU}{m} } }=\frac{eF}{\sqrt{2meU} }=\frac{F}{\sqrt{2U}}\cdot \sqrt{ \frac{e}{m}}$ (9)
Ну теперь подставляем в (9) числа
$I= \frac{F}{ \sqrt{2U} } \sqrt{ \frac{e}{m} } = \frac{10^{-6}}{ \sqrt{2 \cdot 22\cdot 10^3} } \sqrt{ \frac{1,6 \cdot 10^{-19}}{9,11 \cdot 10^{-31}} } =0,1998 \cdot 10^{-2}=1,998 \cdot 10^{-3}$ А≈2 мА

P.S. Идея расчета сходна с идеей вывода основного уравнения МКТ.
Да еще, когда я считал скорость у меня получилось значение порядка 10^7 м/с, если так, то по идее должны сказываться релятивистские эффекты.

Exponena_zn (13.2k баллов) 04 Апр, 18