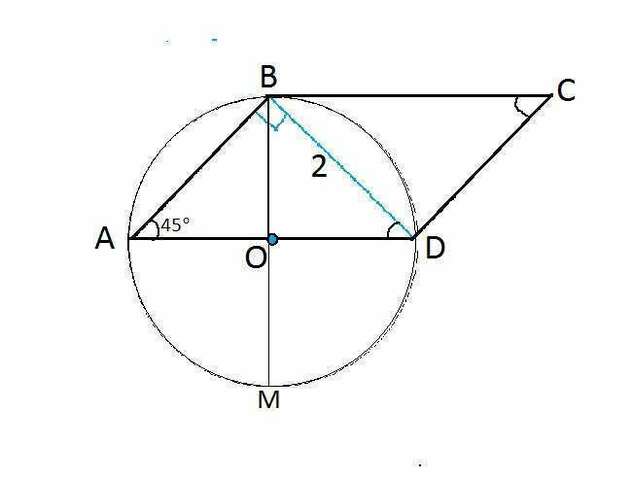
В параллелограмме сумма углов при одной стороне равна 180º.
3π/4=135º, следовательно, острый угол параллелограмма равен 45º.
Треугольник АВD- вписанный, точки А, В и D лежат на окружности. Следовательно, точка В является точкой касания, т.к. в противном случае окружность имела бы с касательной (прямой ВС) две общие точки, что противоречит определению касательной.
Тогда ВМ , проведенный в точку касания - диаметр описанной окружности.
Угол OВС=90º, АВО=45º.⇒ угол АОВ=90º
Хорда АD параллельна ВС и потому перпендикулярна диаметру ВМ. Хорда, перпендикулярная диаметру, делится им пополам. Прямоугольные треугольники АВО и ВDO равны по равным катетам, следовательно, угол ВDО=ВАО=45º, угол АВО=45º, OBD=45º, ⇒ угол ABD= 90º. ⇒ угол ВDС=90º
Треугольник АВД равнобедренный прямоугольный, ВD - перпендикулярна и равна АВ и DC, и является высотой параллелограмма.
S (ABCD)=BD*DC=2*2=4 (ед. площади)