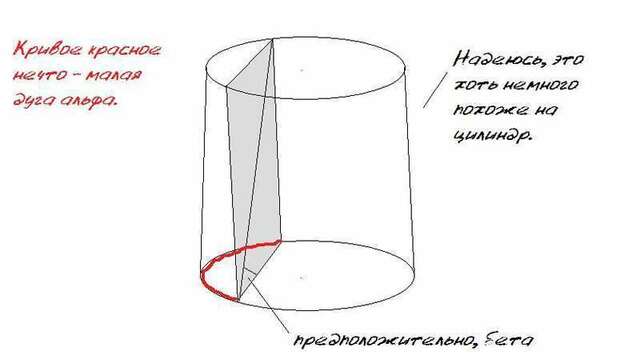
Параллельно оси цилиндра проведена плоскость, которая отсекает от окружности основания меньшую дугу α. Диагональ сечения образует с плоскостью основания угол β. Найдите площадь сечения, если площадь основания равна S.
Кто-нибудь может решить? Спасибо, если кто откликнется.