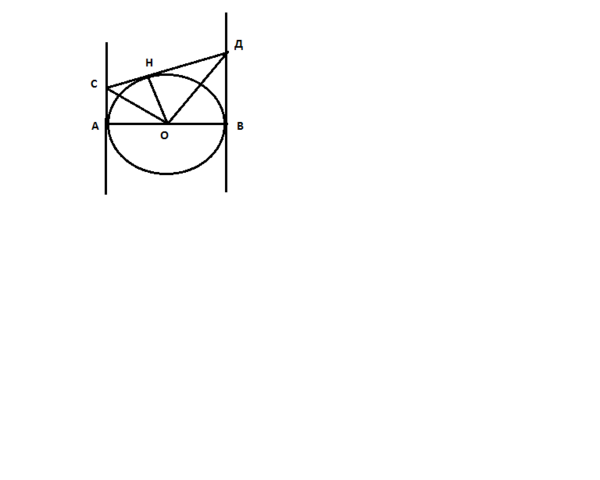
Круг с центром О, диаметр АВ=2ОА=2R
Третья касательная касается круга в точке Н.
Т.к. отрезки касательных к окружности, проведенных из одной точки, равны, то СА=СН и ДВ=ДН
Получается, что круг вписан в ∠АСД и в ∠СДВ, а
если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, т.е. СO - биссектриса ∠АСД.и ДО - биссектриса ∠СДВ.
Также СO - биссектриса ∠АОН и ДО - биссектриса ∠ВОН.
∠АОН и ∠ВОН - смежные, значит СО⊥ДО
В прямоугольном ΔСОД ОН- высота, проведенная из прямого угла к гипотенузе СД (
касательная к окружности перпендикулярна к радиусу, проведенному в точку касания), значит ОН²=СН*ДН=СА*ДВ, ч.т.д