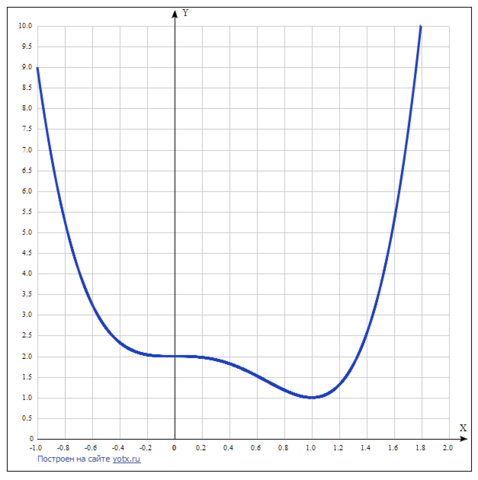
Промежутки монотонности определяются производной функции.
Если производная положительна - функция возрастающая и наоборот.
f' = 12x³ - 12x².
Приравняем производную нулю для определения критических точек.
12x³ - 12x² = 0
12x²(х - 1) = 0
Отсюда получаем 2 критические точки:
х = 0 и х = 1.
Теперь надо определить знаки производной вблизи этих точек.
х = -1 f' = -24
x = 1/2 f' = 12/8 -12/4 = -12/8
x = 2 f' = 96-48 = 48.
Ответ: (-∞ < x <0) функция убывающая,<br> (0 < x <1) функция убывающая,<br> (1 < x < ∞) функция возрастающая.<hr>