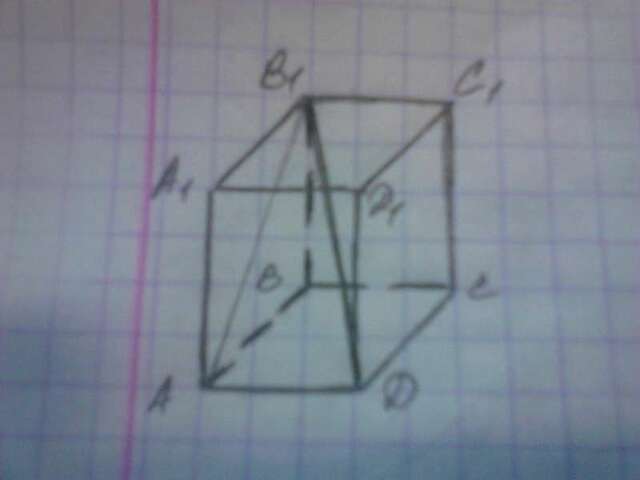
АВСДА1В1С1Д1 - правильная четырёхугольная призма - тогда в основании квадрат.
Диагональ - В1Д, угол В1ДА=30 , тогда из треугольника В1АД:
В1А=1/2В1Д (т.к. лежит напротив угла в 30), тогда В1А=4/2=2 см
тогда по т Пиф найдём АД:
АД=корень из(16-4)=корень из 12 = 2корня из 3 см
Из треугольника АВД: АД=АВ=2корня из 3 см (онование квадрат), тогда
ВД=корень из(12+12)=корень из 24= 2 корня из 6 см
Из треугольника В1ДВ: ВД=2 корня из 6, В1Д=4, найдём В1В:
В1В= корень из(24-16)=корень из 8=2корня из 2 см
Sбок пов=4*Sбок грани
Sбок грани=АВ*ВВ1=2корня из 3 * 2корня из 2=4 корня из 6 см квадратных, тогда
4*Sбок грани=4 корня из 6*4=16 корней из 6
Ответ: площадь боковой поверхности призмы равна 16 корней из 6 см квадр.
P.S. площадь боковой пов-ти не путать с площадью полной поверхности !!!!!!!!!!!!!
Удачи ! )