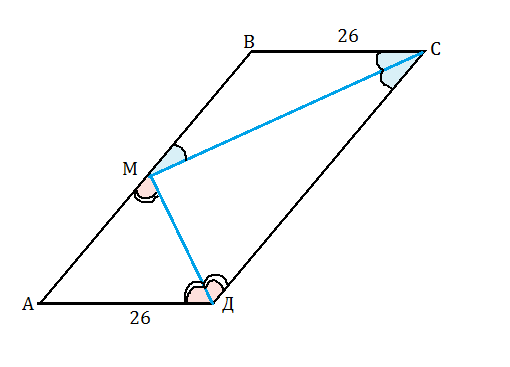
Пусть этот параллелограмм АВСД.
СМ и ДМ - биссектрисы.
АМ||СД, СМ - секущая.
Накрестлежащие углы при пересечении параллельных прямых секущей равны. Угол ВМС=углу МСД.
Но так как СМ биссектриса и угол МСД=ВСМ, то все эти три угла равны. Из равенства углов при основании СМ треугольника МВС следует. что этот треугольник - равнобедренный. МВ=Вс=26.
Точно также доказывается равенство сторон АМ и АД треугольника АМД.
Следовательно, большая сторона АВ=СД=АМ+МВ=26+26=52.
--------
Замечу, что биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ( иногда сюда входят продолжения сторон). Это свойство биссектрисы пригодится при решении многих задач.