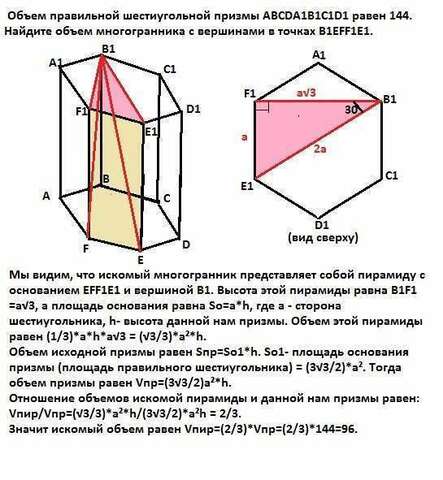
Мы видим, что искомый многогранник представляет собой пирамиду с основанием EFF1E1 и вершиной В1. Высота этой пирамиды равна В1F1=а√3, а площадь основания равна So=а*h, где а - сторона шестиугольника, h- высота данной нам призмы.
Объем этой пирамиды равен (1/3)*а*h*а√3 = (√3/3)*а²*h.
Объем исходной призмы равен Sпр=Sо1*h. Sо1- площадь основания призмы (площадь правильного шестиугольника) = (3√3/2)*а². Тогда объем призмы равен Vпр=(3√3/2)а²*h.
Отношение объемов искомой пирамиды и данной нам призмы равен:
Vпир/Vпр=(√3/3)*а²*h/(3√3/2)*а²h = 2/3.
Значит искомый объем равен Vпир=(2/3)*Vпр=(2/3)*144=96.
Ответ: объем многогранника В1EFF1E1 равен 96.