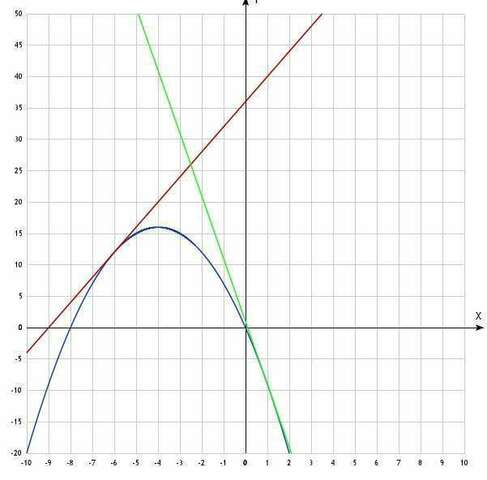
F(x)=-8x-x^2
f(x)=-8x-x^2
f(x1)=-8*(-6)-(-6)^2=12
f(x2)=-8*1-(-1)^2=-9
f '(x)=-8-2x
f '(x1)=-2*(-6)-8=4
f '(x2)=-2*1-8=-10
y=f(x1)+f '(x1)*(x-x1)=12+4(x-(-6))=4x+36
y=f(x2)+f '(x2)*(x-x2)=-9-10(x-1)=-10x+1
точка пересечения касательных -высота тр-ка 4x+36=-10x+1 --->x=-5/2
точки пересечения с У (х=0)
у1=36у2=1длина основания 36-1=35
S=0.5*2.5*35=43,75 кв.ед.