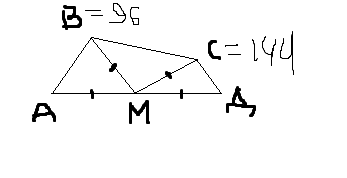Середина м стороны ад выпуклого четырехугольника авсд равноудалена от всех его вершин....

Question

Середина м стороны ад выпуклого четырехугольника авсд равноудалена от всех его вершин. найдите ад если вс=7 а углы в и с четырехугольника равны соответственно 96 и 144

Answer 1

Рисунок внизу.

м равноудалена от вершин, значит, около этого четырехугольника можно описать окружность, значит, сумма противоположных углов равна 180 (по свойству).

А=180-С=36

ΔАМВ - равнобедренный ⇒ АВМ=А=36

МВС=В-АВМ=60

В равнобедренном ΔВМС угол 60 ⇒ он равносторонний ⇒ ВС=МС=7

АД=2МД=2МС=14

Ответ:14

---