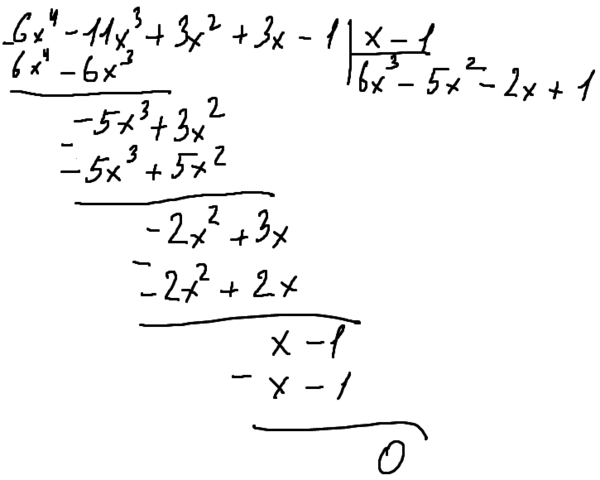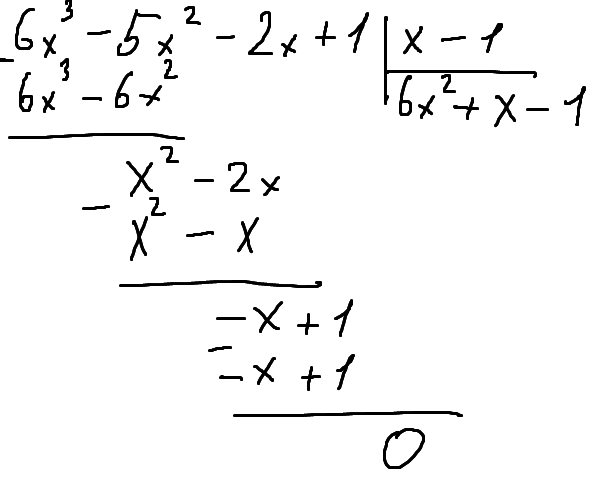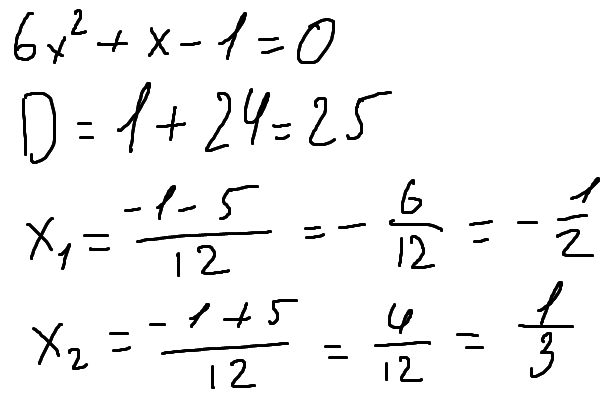Получается уравнение четвёртой степени. Оно решается по теореме Безу.
Во-первых, нам нужно определить "корень". Для этого надо найти делители свободного члена, которым является 3. Слава богу математики, делителя всего 4: плюс-минус 1, плюс-минус 3. Подставив каждый из них в уравнение, получим, что "корнем" является 1.
Во-вторых, потребуется деление «уголком»: это то же самое, что решать делением в столбик, только в качестве ответа нарисуется уравнение третьей степени, которое аналогичным способом нужно будет разобрать до уравнения второй степени и решить его старым-добрым дискриминантом или Виетом.
Файлы в порядке решения уравнения: