Сделаем рисунки к задаче. С ними легче ее решить.
Плоскость равностороннего треугольника, вершины которого лежат на поверхности шара, лежит в плоскости сечения этого шара.(Во всяком случае в школьном разделе геометрии)
Радиус этого сечения равен радиусу описанной около треугольника окружности.
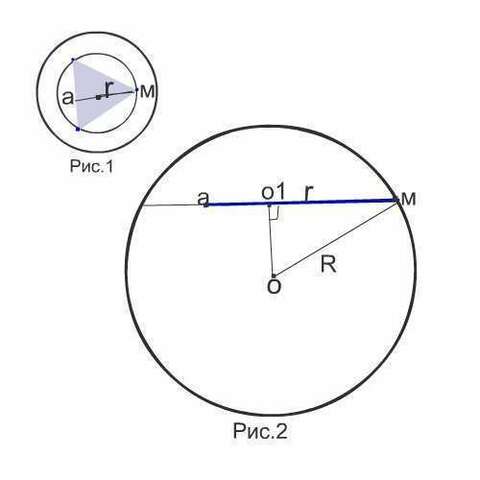
Если смотреть на шар сверху, то это может выглядеть как на рис. 1
Радиус описанной около равностороннего треугольника окружности равен ⅔ его высоты.
Высота равностороннего треугольника находится по формуле:
h=(а√3):2, где а - сторона этого треугольника.
r=⅔ (а√3):2=⅔ (18√3):2=2(18√3):6=6√3
Рассмотрим на рис.2 сечение шара, перпендикулярное плоскости треугольника, и соответсвенно сечения, в плоскости которого этот треугольник лежит.
Расстояние Оо1 равно по условию задачи 6 см
о1м=r=6√3
Из прямоугольного треугольника Оо1м найдем его гипотенузу = R
R²=о1м²+о1О²=108+36=144
R=√144=12 см
Площадь поверхности шара равна учетверенной площади большого круга:
S=4 π R²
S=4 π·144= 576 см²