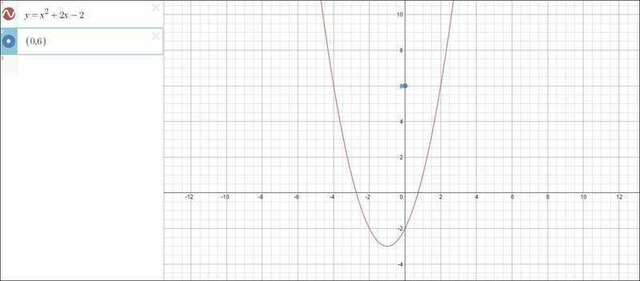
1)x²+2x-2=x²+2x+1-3=(x+1)²-3 т.е. вершина параболы находится в точке (-1;3) и правая ветвь параболы пересекает ось У в точке (0;-2). Следовательно точка А(0;6) находится внутри параболы и через эту точку провести касательную к параболе у=х²+2х-2 не представляется возможным.
2)Положим, что прямая y=kx+b касается графика функции f(x) в точке с абсциссой х₁, а графика функции g(x) в точке с абсциссой х₂.
Уравнение касательной к графику функции f(x)=x²+2x+4 :
y=f'(x₁)(x-x₁)+f(x₁). где f'(x₁)=2x+2|x=x₁|=2x₁+2
y=(2x₁+2)(x-x₁)+x₁²+2x₁+4
y=2x₁x-2x₁²+2x-2x₁+x₁²+2x₁+4
y=(2x₁+2)x+4-x₁² (1)
Уравнение касательной к графику функции g(x)=-x²-1:
y=g'(x₂)(x-x₂)+g(x₂), где g'(x₂)=-2x|x=x₂|=-2x₂
y=-2x₂(x-x₂)-x₂²-1
y=-2x₂x+2x₂²-x₂²-1
y=-2x₂x+x₂²-1 (2)
поскольку уравнения (1) и (2) - это уравнения одной и той же прямой, составим систему уравнений из условия равенства угловых коэффициентов и свободных членов:
2x₁+2=-2x₂ x₁=-x₂-1 x₁=-x₂-1
{ { {
4-x₁²=x₂²-1 4-(x₂+1)²-x₂²+1=0 4-x₂²-2x-1-x₂²+1=0
x₁=-x₂-1 x₁=-x₂-1 x₁=-x₂-1
{ { {
-2x₂²-2x+4=0 x₂²+x₂-2=0 x₂=-2
[
x₂=1
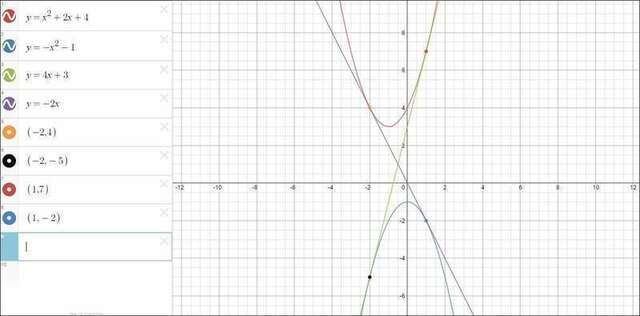
имеем два решения: x₁=1; x₂=-2 и x₁=-2; x₂=1
уравнение первой касательной: y=4x+3
уравнение второй касательной: у=-2x