Сторона АВ квадрата АВСD, равная 13 см, лежит в плоскости. Расстояние от прямой СD до...

Дано: a=13, d=2

Найти: k-?

Решение:

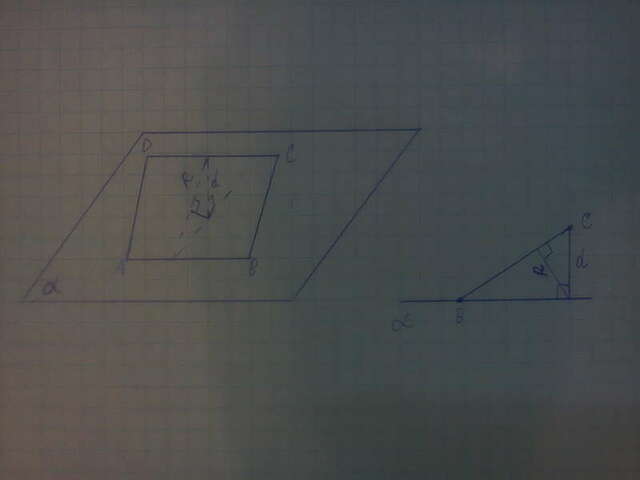
Делаем чертеж (во вложениях).

В изометрии плохо видно что нам нужно найти, поэтому делаем фронтальную плоскость(вид сбоку). Теперь видно что из себя представляет k и как его найти.

Во первых найдем синус между плоскостью и квадратом:

$sin\beta*a=d\\ sin\beta=\frac{d}{a}\\ sin\beta=\frac{2}{13}$

Теперь найдем величину малого отрезка, который выходит при делении BC перпендикуляром k. Назовем его CE

Сразу скажем что угол между плоскостью и квадратом равен углу между k и d, т.к. угол C общий и в этих треугольниках есть прямые углы.

$d*sin\beta = CE\\ 2*\frac{2}{13}=\frac{4}{13}\\ CE=\frac{4}{13}$

Теперь можем найти k по теор. Пифагора

$k=\sqrt{d^2-CE^2}=\sqrt{2^2-(\frac{4}{13})^2}=\frac{2\sqrt{165}}{13}$