На гипотенузе AB прямоугольного треугольника ABC , выбрана точка K , для которой CK=BC....

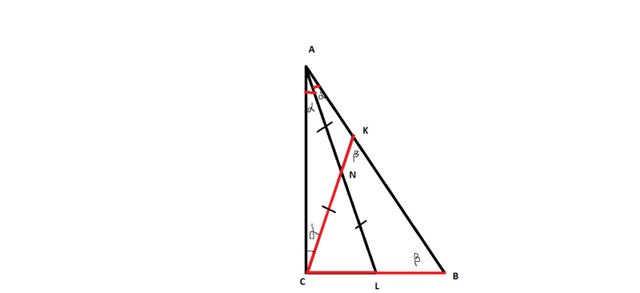
См. рисунок. думаю, будет понятно. Задачка , вроде, не трудная.
итак, СК=СВ - треуг. ВСК равнобедр, углы при его основании равны. Я их обозначил $\beta$
AL- биссектриса, то равные углы я обозначил как $\alpha$

АN=NL значит, т. N для прямоуг.треугольника ACL является центром описанной окружности, значит, AN=NL=NC , значит, треуг. ANC равнобедренный, и углы при основании равны , и равны $\alpha$
тепиерь, угол СКВ внешний для треуг. АКС, значит угол СКВ= $\beta$ = $\alpha +2 \alpha =3 \alpha$
из прямоуг. треуг. АВС угол А+угол В=90

$2 \alpha +3 \alpha =90 \\ \alpha =18 \\ A=2 \alpha =36 \\ B=3 \alpha =54$

** гипотенузе AB прямоугольного треугольника ABC , выбрана точка K , для которой CK=BC....