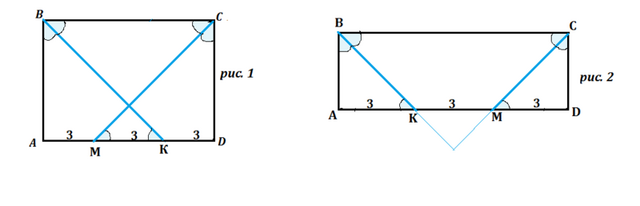
Биссектрисы двух углов прямоугольника делят его сторону на три части, каждая из которых равна 3 см. Найдите периметр прямоугольника. Сколько решений имеет задача?
-----------
Биссектриса угла параллелограмма ( а прямоугольник - параллелограмм) отсекает от него равнобедренный треугольник. Это полезно запомнить.
Пояснение:
Проведем биссектрисы из углов В и С.
Рассмотрим рисунки.
В треугольнике АВК угол АКВ равен углу СВК прямоугольника, как накрестлежащие при параллельных прямых ВС и АD и секущей ВК.
Но угол СВК=углу АВК - по свойству биссектрисы. Следовательно, угол АКВ=углу АВК и АВ=АК как стороны равнобедренного треугольника.
Решение 1.
Биссектрисы пересекаются внутри прямоугольника. (рис. 1)
Тогда АВ=АМ+МК=6 см
CD=AB=6 см
ВС=АD =3*3=9 см
Периметр прямоугольника равен 2(АВ+АD)=2*15=30 см
Решение 2.
Биссектрисы пересекаются вне прямоугольника. (рис.2)
Тогда АВ=АК=3 см, СD=MD=3 см
ВС=АD =3*3=9 см
Периметр прямоугольника равен 2(АВ+СD)=2*12=24 см