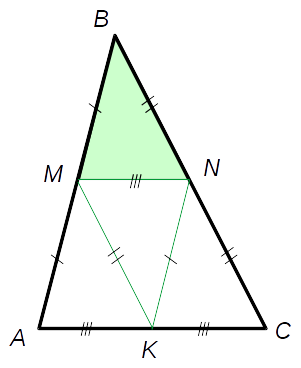
Набросаем рисунок. ABC данный треугольник, MN - средняя линия.
Площадь закрашенного маленького треугольника нам известна.
Дополнительно построим еще две средние линии NK, MK.
Каждая средняя линия делит свои "боковые" стороны пополам. Вспоминаем, что длина средней линии равна половине длины "своего" основания. Отмечаем равные отрезки.
(Не буду подробно расписывать кто равен кому и почему. )
Получаем, что наш исходный треугольник разбит на 4 равных маленьких треугольничка. (они равны между собой по 3м сторонам). Площадь треугольника MBN задана по условию, а раз треугольники равны то и площадь остальных нам известна.
Трапеция AMNB, как видно состоит из 3х одинаковых треугольников, площадь каждого из них равна 2. Ну значит площадь трапеции 2*3=6