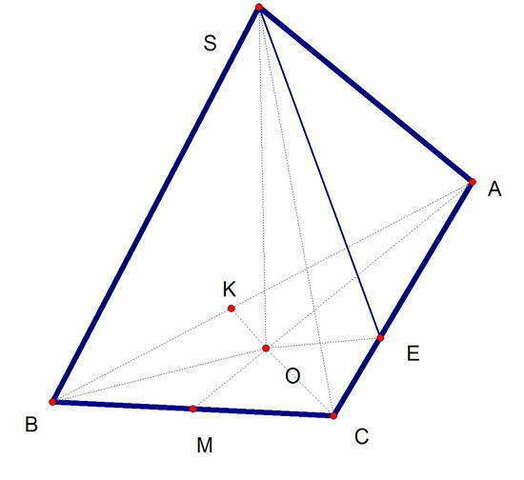
(к чертежу - так как все грани наклонены под одним углом к основанию, то основание высоты совпадает с точкой пересечения биссектрис, угол А = альфа, ВС=а)
Площадь полной поверхности складывается из площади основания и площади боковой поверхности(суммы площадей боковых граней). Существует теорема, что площадь грани равна площади проекции этой грани, деленной на угол наклона грани к плоскости проекции
То есть S грани SBC= S трВОС/cos бета
И так же с остальными гранями, поскольку все они наклонены под углом бета
Поэтому S боковой поверхности равна S тр АВС/cosбета
Остается найти площадь АВС
АМ -биссектриса, поэтому угол МАС=альфа/2
Из треугольника АМС находим АМ=МС*ctg(альфа/2), МС=а/2 и ищем площадь
Остальное не представляет трудностей