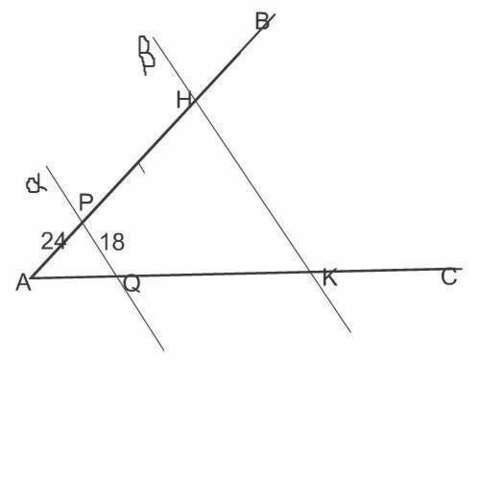
Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно в точках Р и Н, а сторону АС этого угла - соотвптственно в точках Q и К
Найдите:
а)АН и АК если РН= 2РА, РН = 12 см, AQ = 5 см
Задача на подобие треугольников.
Рассмотрим рисунок.
Стороны угла АВС и параллельные плоскости ( на рисунке они изображены прямыми α и β ) образуют пересечением два подобных треугольника,
так как их углы при параллельных основаниях равны по свойству параллельных прямых и секущей.
В треугольнике АНК дано, что отрезок РН = 2 РА.
РН=12, ⇒
РА=12:2=6 см
АН =12+6=18 см
Сторона АН ᐃ АВС пропорциональна стороне АР ᐃ APQ
k=18:6=3
Так как рассматриваемые треугольники подобны, то
АК:АQ=3
АQ=5, ⇒
АК=5·3=15см
б) НК и АН, если PQ = 18 см, АР = 24 см, АН = 3/2 РН
АН = 3/2 РН ⇒
РН=2/3 АН
АР=1/3 АН =24 см
АН=24·3=72 см
Так как k=3,
PQ=1/3 НК ⇒
НК=18·3=54 см