Найдите основание AD равнобедренной трапеции ABCD если BC равно 20 сантиметров AB равно...

Question

Найдите основание AD равнобедренной трапеции ABCD если BC равно 20 сантиметров AB равно 24 см и угол D равен 60 градусов

Answer 1

Проведем две высоты: ВК и СМ
рассмотрим треугольник АВК: угол К прямой, угол АВК =90-60=30, значит АК=АВ:2=24:2=12
 и МД=12, КМ=ВС=20
АД=АК+КМ+МД=12+20+12=44
ОТВЕТ:АД=44см

Answer 2

Дано:
ABCD - равнобедренная трапеция (AB=BC),
BC=20 см,
AB=24 см,
∠D=60°
Найти: AD.

Решение:
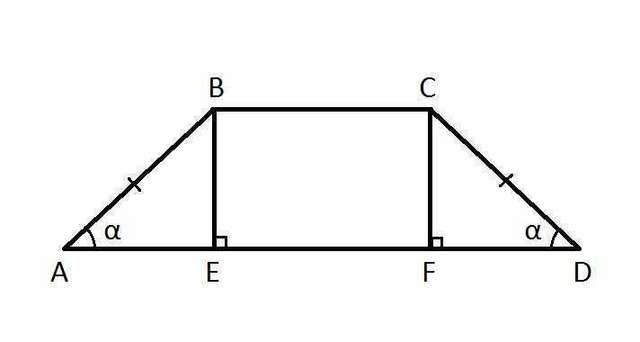
Из т. В и т. С опустим высоты ВЕ и СF на основание AD. По условию трапеция равнобедренная, значит AB=CD=24 см, также углы при основании равны: ∠A=∠D=α=60°.
AD=AE+EF+FD. Так как ΔАВЕ=ΔDCF, то AE=DF, тогда AD=2AE+EF.
По построению получен прямоугольник EBCF, в котором BC=EF, тогда AD=2AE+BC.
Найдём АЕ из ΔАВЕ. ΔАВЕ - прямоугольный по построению, в котором АЕ - прилежащий катет к ∠α, АВ - гипотенуза. По определению косинуса cosα=АЕ/АВ ⇒ АЕ=АВcosα.
Тогда AD=2ABcosα+BC.
AD=2*24*cos60°+20=44 (см).
Ответ: 44 см.

---