Из точки A лежащей ** окружности радиуса r проведены две хорды AC и AB . эти хорды лежат...

0 голосов
63 просмотров

Из точки A лежащей на окружности радиуса r проведены две хорды AC и AB . эти хорды лежат по одну сторону от диаметра окружности проходящнй через точку A . дана длина b большей хорды и угол BAC=a. найти радиус окружности которая касается хорд AB и AC и дуги BC

Геометрия (15 баллов) | 63 просмотров
Дан 1 ответ
0 голосов
Правильный ответ

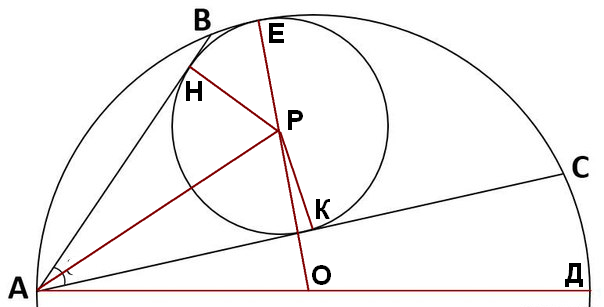
Окружность с центром О радиусом АО=ОД=r
хорда AC=b, Окружность с центром Р  касается АВ в точке Н, АС - в точке К и дуги ВС * в точке Е. Радиус этой окружности РН=РЕ=РК=R.
Рассмотрим ΔАНР и АКР: они прямоугольные , т.к. точку касания), и равны по трем сторонам (радиусы РН=РК, АР-общая, АН=АК как отрезки касательных из одной точки).
Значит <НАP=<КАP=<ВАC/2=α/2<br>AP=PK/sin (α/2)=R/sin (α/2).
Вписанный угол АСД опирается на диаметр, значит он прямой.
Следовательно, из прямоугольного ΔАСД найдем угол САД, обозначим его β:
cos β=АС/АД=b/2r, sin β=√(1-cos²β)=√(1-b²/4r²)=√(4r²-b²)/2r.
Из ΔАОР по т.косинусов найдем РО, исходя из того, что
РО=ЕО-ЕР=r-R и сos (α/2+β)=сos (α/2)*сos β-sin (α/2)*sin β=сos (α/2)*b/2r-sin (α/2)*√(4r²-b²)/2r

РО²=АО²+АР²-2*АО*АР*сos (α/2+β)
Подставляем данные:

(r-R)^{2} = r^{2} + \frac{R ^{2} }{sin^{2} \frac{ \alpha }{2} }-2r* \frac{R}{sin \frac{ \alpha }{2} }*(cos \frac{ \alpha }{2} * \frac{b}{2r} -sin \frac{ \alpha }{2}* \frac{ \sqrt{4 r^{2}- b^{2} } }{2r}

r^{2}-2rR+R^{2} = r^{2} + \frac{R^{2} }{sin^{2} \frac{ \alpha }{2} }- \frac{R*cos \frac{ \alpha }{2}*b}{sin \frac{ \alpha }{2} }+R*\sqrt{4 r^{2}- b^{2} }

R^{2}(1 - \frac{1 }{sin^{2} \frac{ \alpha }{2} })=R(2r- \frac{cos \frac{ \alpha }{2}*b}{sin \frac{ \alpha }{2} }+\sqrt{4 r^{2}- b^{2} })

R=(2r- \frac{cos \frac{ \alpha }{2}*b}{sin \frac{ \alpha }{2} }+\sqrt{4 r^{2}- b^{2} })/( - \frac{cos^{2} \frac{ \alpha }{2} }{sin^{2} \frac{ \alpha }{2} })

R=(\frac{b}{tg \frac{ \alpha }{2} }-2r-\sqrt{4 r^{2}- b^{2} })*tg^{2} \frac{ \alpha }{2}

image
(101k баллов)
Похожие задачи