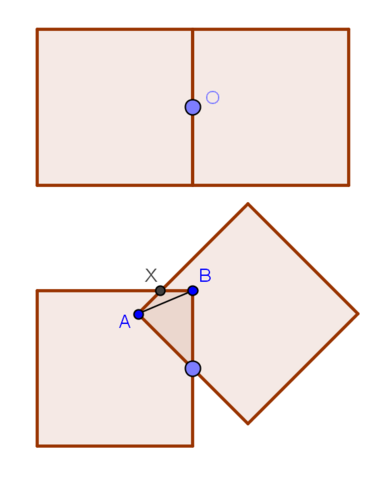
Рассмотрим треугольник OAB. Угол O в нем равен 45 градусов, по теореме косинусов находим АВ:
AB^2=2*1/2(1-cos45)=1-sqrt(2)/2=(2-sqrt(2))/2
Угол А здесь равен углу В. Синус угла А найдем так:
S=0.5OA*OB*sin45=0.5AB*AO*sinA
sinA=OA*OB*sin45/(AB*AO)=0.5*0.5*sqrt(2)/2/((2-sqrt(2))/2*0.5)=0.5*sqrt(2)/(2-sqrt(2))
Треугольник АВХ равнобедренный. Понятно, что АХ=ВХ=0.5AB/cos(XAB)=0.5*AB/sin(OAB)
AX=(2-sqrt(2))/4 / (0.5*sqrt(2)/(2-sqrt(2)))=(2-sqrt(2))^2/(2sqrt(2))=0.5(3sqrt(2)-4)
Тогда периметр равен 8*1-2*АХ-2*0.5=8-(3sqrt(2)-4)-1=11-3sqrt(2)